@Book{Knuth2006,
  Author         = {Knuth, Donald E.},
  Title          = {{Generating All Trees: History of Combinatorial Generation}},
  Bookseries     = {{The Art of Computer Programming}},
  Volume         = {4},
  Note           = {fascicle 4},
  Publisher      = {Routledge, Kegan \& Paul},
  Address        = {London, Boston and Henley},
  Year           = 2006
}

p.3
===

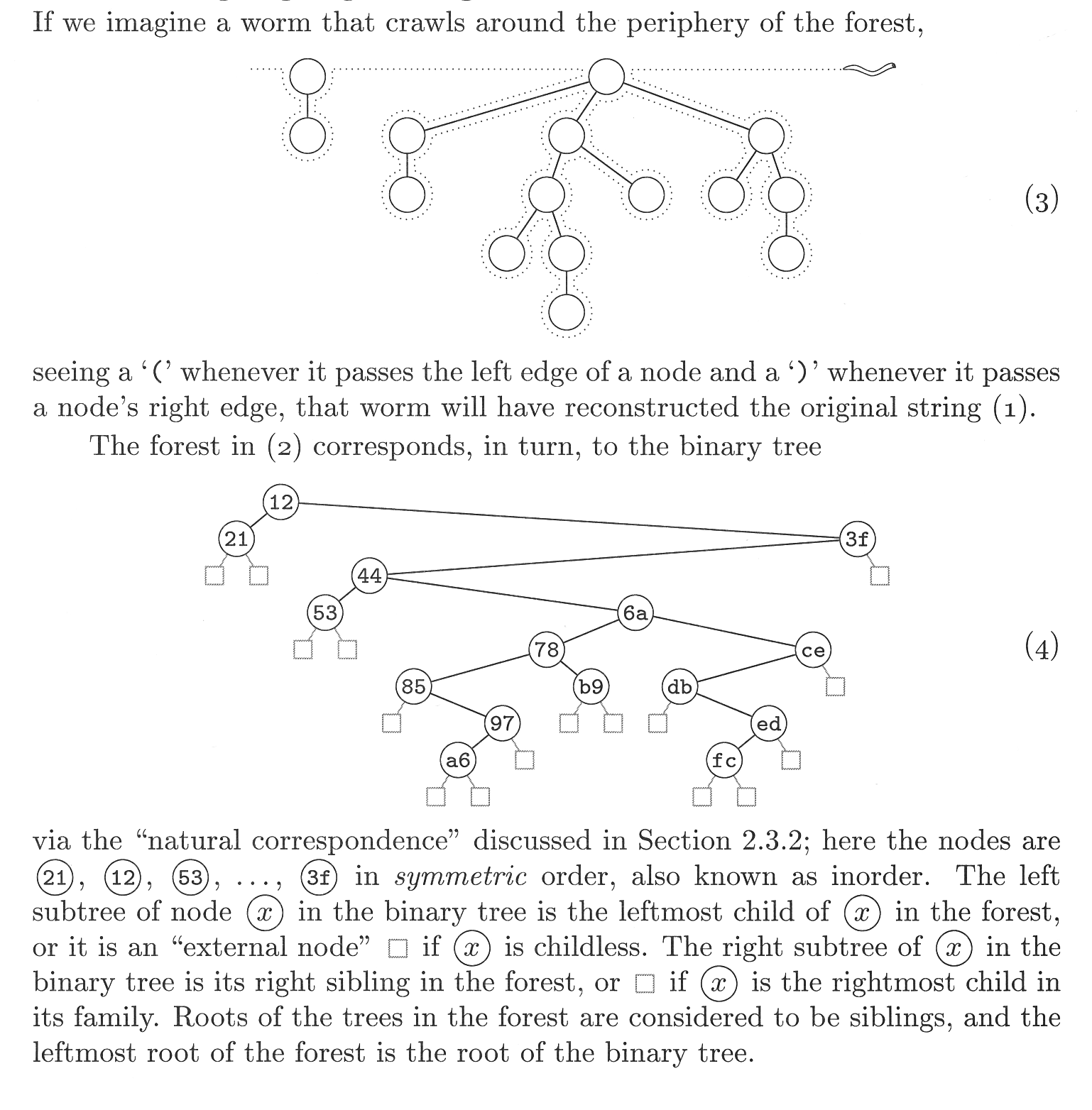
If we imagine a worm that crawls around the periphery of the forest, seeing a ‘(’ whenever it passes the left edge of a node and a ‘)’ whenever it passes a node’s right edge, that worm will have reconstructed the original string (1).


p.35
====

25. [30] (Pruning and grafting.) Representing binary trees as in Algorithm B, design an algorithm that visits all link tables l1...ln and r1...rn in such a way that, between visits, exactly one link changes from j to 0 and another from 0 to j, for some index j. (In other words, every step removes some subtree j from the binary tree and places it elsewhere, preserving preorder).



0 Hornbeam
1 Beech
2 Maple
3 
4
5 
6
7
8
9 Oak
10
11 Linden
12 
13

https://www.flickr.com/photos/foam/20976922469/